Where are all the triangular churches?

My wife and I were discussing geometric church plans the other day. Looking through a wide range of shapes, she asked, "Why are there no triangular churches?" My first thought was, of course there are. I swore I'd seen many; I've seen just about everything else. But then I tried to name one. I was stumped.

Triangles are such brilliant structural forms. They show up in section all over the place. I wrote a post discussing the tent-form or a-frame that was immensely popular in the US in the 1960s and 1970s that is simply a triangle in section. There are plenty of examples of structural elements, roofs, etc. But what about plans?

Plans were an obsession with church architects in the 20th century, especially 1940s-1960s in Germany. Architecturally, it was an incredibly dramatic formal move to modify the plan of a church. Liturgically, it was seen as a clear way to intentionally modify the arrangement of the different participants and objects in the liturgy to express the desired relationships between them. I suspect the fascination with plans also had to do with the iconic nature of The Church Incarnate and improved technology making it easier to reproduce plans in books.

So I went looking in a few of my go-to plan-happy books. There are of course no shortage of wedge-shaped plans following on radial auditorium arrangements. But we're looking for equilateral triangles. I found a number of interesting plans constructed from compositions of triangles or tripartite in various ways. Here is the plan of the Evangelical Church of the Resurrection, Rottach-Egern, Germany from 1954.

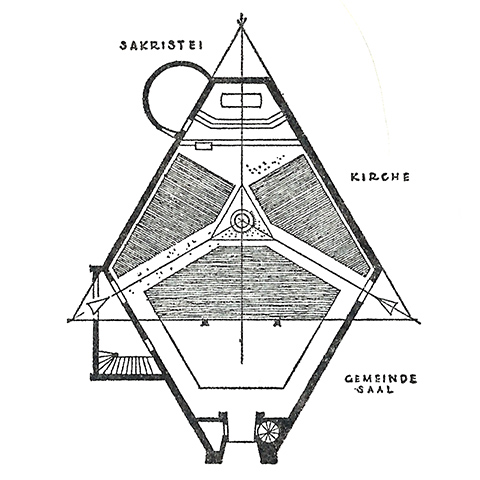
But take a look at the satellite photo. That triangle is a construction tool only and has little to do with the spatial form of the building. Not sure what the triangular object in the center is, either. There are also plenty of modified triangles. Here is an unbuilt design based on an equilateral triangle with its vertices truncated. Or you could describe it as an equiangular hexagon with unequal lengths. But given the triangular sanctuary plinth and three seating sections, I'd call it triangular.

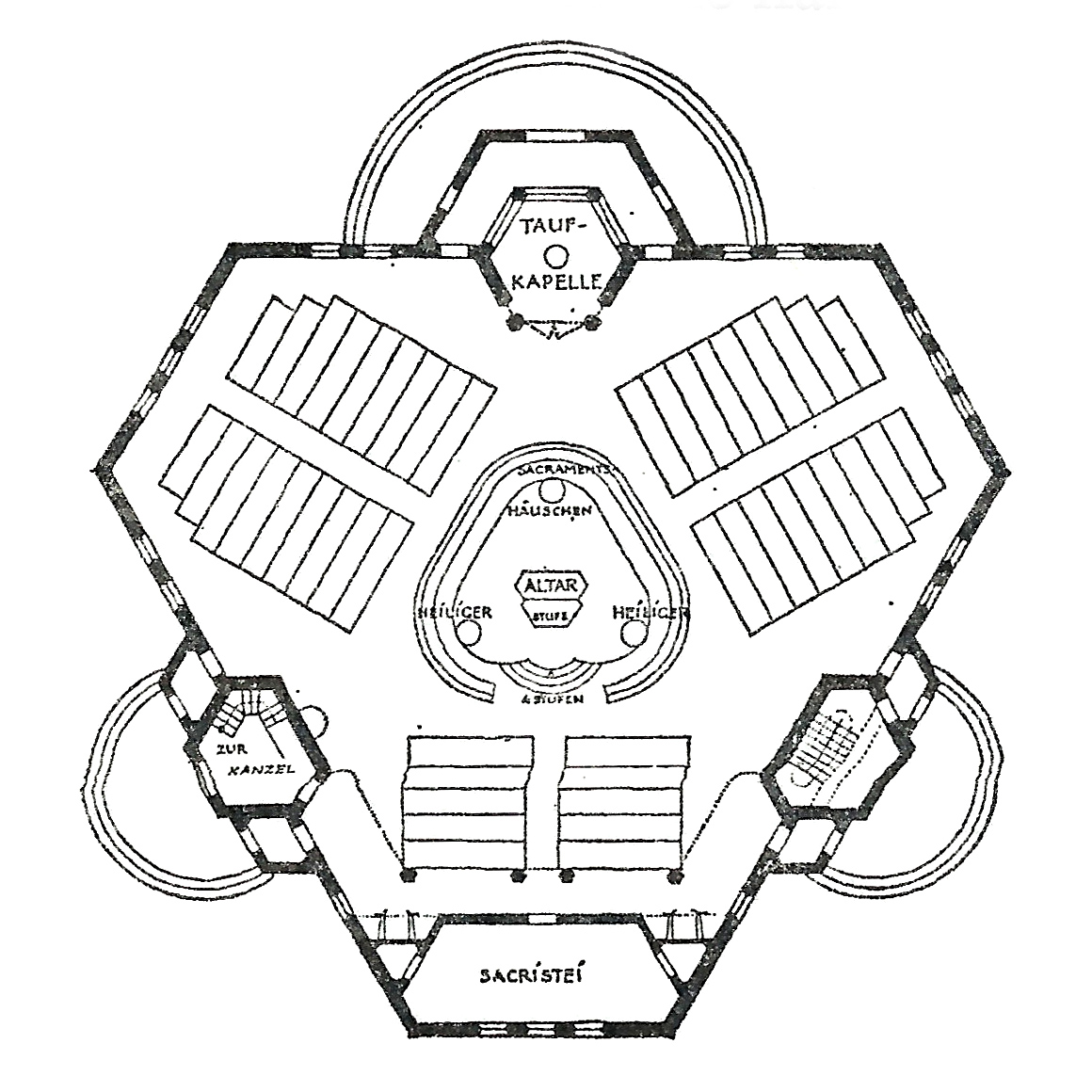
One possible explanation for not using an equilateral triangle plan might be the acute interior angles—in the trade we call those "dead cat spaces." This plan seems to be a solution to that problem. But looking through plans, there are no shortage of irregular polygons with acute angles. (Perhaps only an architect who would be drawn to regular polygons would be offended by acute interior angles?) It also shows a potential weakness of a center-altar triangular plan. The three banks of benches here are more isolated than in one surrounded on four or more sides, or on three adjacent sides of a square center. And it is impossible to bring them together in this configuration, which works against the image of "gathering around" the altar. Now here is the winner. Still not a regular equilateral triangle, but something even more geometrically idiosyncratic. Behold, the Reuleaux Triangle Church:

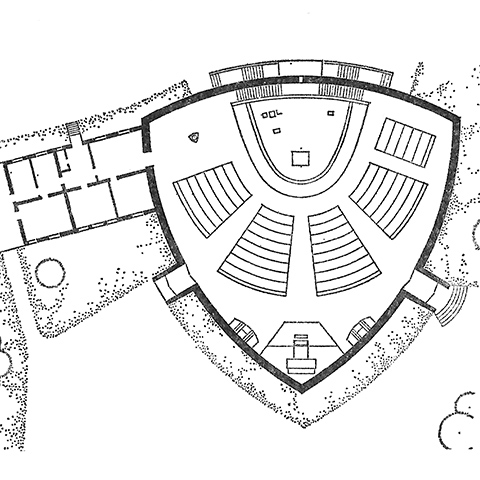
That is the plan for the Church of St Augustine in Bonn-Duisdorf, Germany designed by Stefan Leuer in 1961. Here's the google maps and street view. A Reuleaux triangle is a fascinating bit of geometry, not unlike a squircle. (Actually, it is not at all like a squircle, other than in level of geometric coolness... I just wanted to say squircle.) It is what is known as a "curve of constant width," which means that as it rotates along a surface, the height from the surface to the topmost point on the curve remains constant. What's more, it can be rotated inside a square (unlike a circle, the center is not stationary, but also rotates as it is not equidistant from all points because it's not a circle (sorry for the tautology)). As it rotates, it covers 98.77% of the area of the square. The practical upshot of this is that you can create a drill bit that drills (almost) square holes. Observe:

[youtube_sc url="http://youtu.be/L5AzbDJ7KYI?t=5s" width="480"]

Here is a video that expands on the curve of constant width and expands it into three dimensional solids of constant width:

[youtube_sc url="http://www.youtube.com/watch?v=cUCSSJwO3GU" width="480"]

But all of that is an aside when we consider what the Reuleaux triangle might mean for architecture given that the church does not rotate. The most significant property is in its construction from polygonal and circular components. The most compelling church are in some way hybrids of complementary—if not contradicting—concepts that invoke and then challenge familiarity. Scripture does this, the liturgy does this, and any sufficiently developed theology does this.

The synthesis of angular and circular profiles in plan is on the simple side. Of course, an elegant plan is a necessary but insufficient criteria for a good building and for an effective liturgical arrangement. But it does appear to have deeper implications. For one, it provides the radial seating without sacrificing a grand, dominant sanctuary and focal wall. The auditorium-derived radial seating concept has benefits for lines of sight, audibility, and proximity, but those often come at the cost of a smaller sanctuary tucked in a corner. Rotate the arrangement 60º and it is closer to the typical radial arrangement.

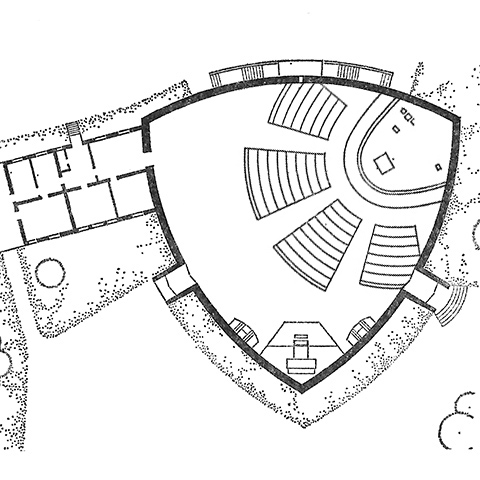
Which is not to say this could not also work, and the curved segments of the Releaux triangle lend a more gracious openness compared to the angular example in Rottach-Egern. But the additional seats needed to make up what I deleted end up further from the altar. As designed it, it puts the width where it is most needed to put the greatest part of the congregation near to the sanctuary.

The comparison of these two versions reveals another contrast in the orientation and directionality created by this shape. In either configuration it acts as a circle with a pointed axis—a clever synthesis of Schwarz's first two plans plus a bit of the typically-parabolic "dark chalice." The corner sanctuary has a stronger "militant" directionality from the image of a ship's prow (prora navis... and we've come back around to the nave). The original has a potential for greater subtlety in its axis. The forward movement could be more of a forward embrace coming from the bi-directionality of point and line.

I say could be, because to make these images effective relies ultimately on their spatial projection. Without direct experience, or at least interior photographs, it is impossible to comment on that component. Again, here is the danger of fixating on plan. Even if we argue that the plan contains the more fundamental truth of the arrangement, it is not the more immediately experienced. There is something we can say generally about the Reuleaux triangle's projection into three dimensions. The idea of being both angular and circular gives the corners an unexpected smoothness without losing the sharp definition, an appropriate gesture for a church interior. A slight variation on this theme would to round the corners to create three parabolas, borrowing from that spatial indeterminacy in each corner. That appears to be the case with Kuratie Heilig Geist (Holy Spirit), Würzburg.

The Reuleaux triangle is a fascinating potential shape for a church that allows the plan to take on the advantages of a number of other arrangements. I would like to see more examples of its use. And if you know of any equilateral triangle plans, please share them in the comments.

UPDATE.

Two church buildings with triangular plans came up recently on one of my favorite tumblrs, Architecture of Doom.